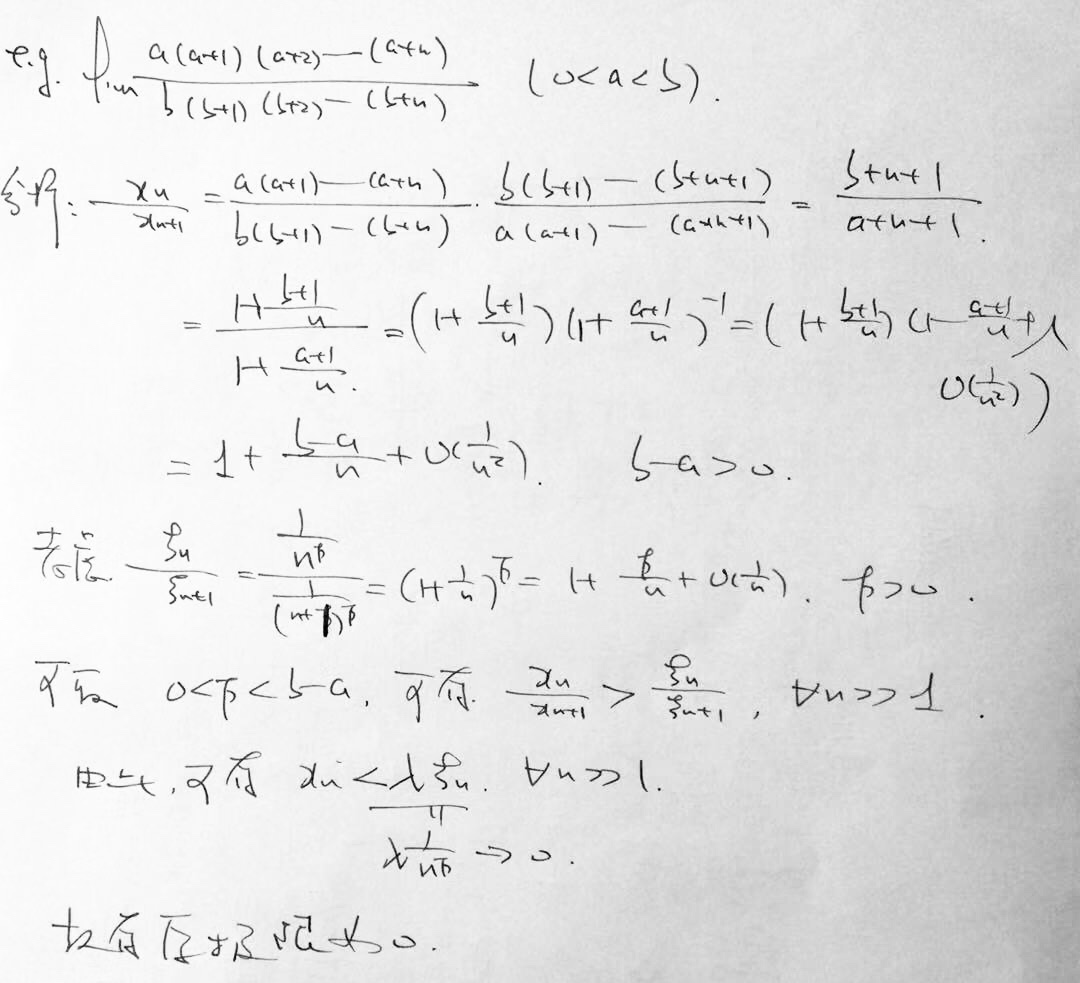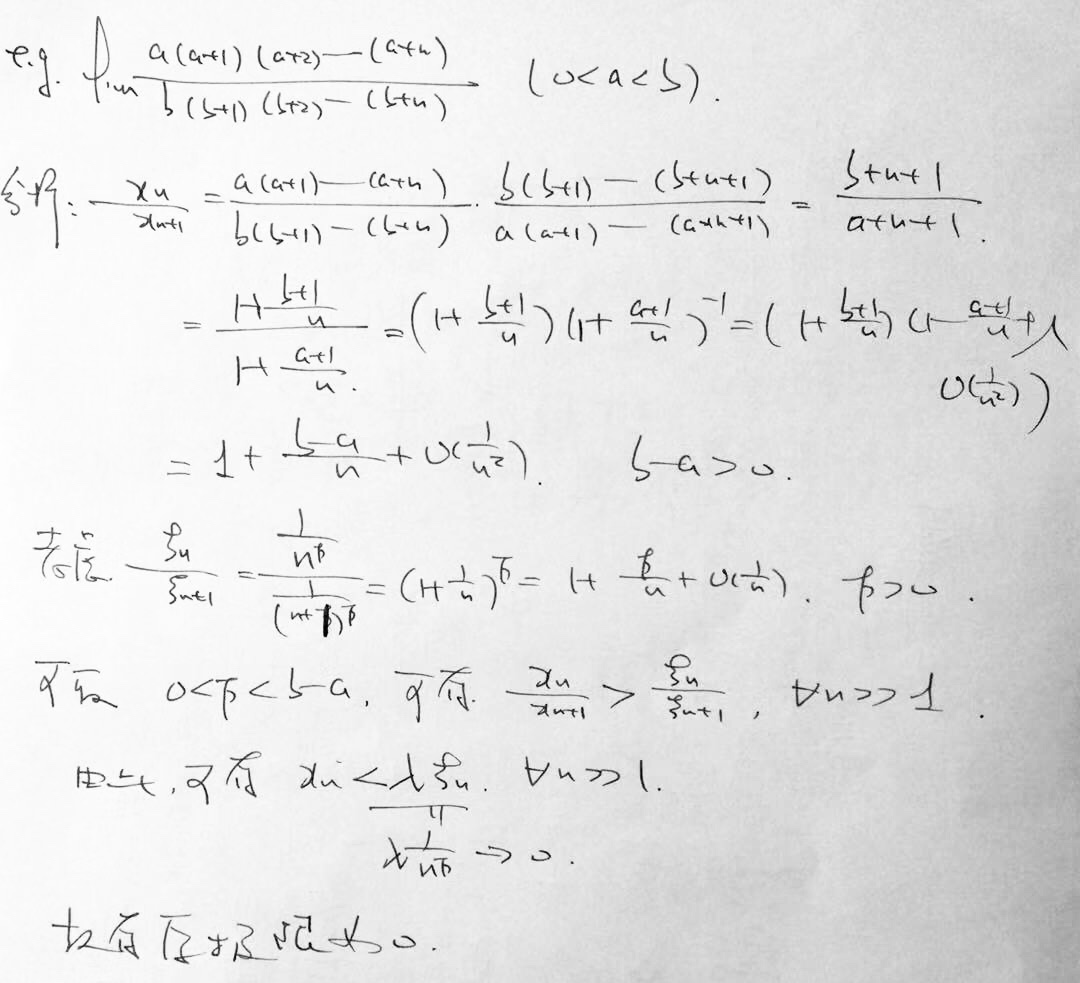已知 $0 < a < b \in \mathbb R$，求：

$$ \lim_{n \rightarrow \infty} \prod_{k = 0}^n {a + k \over b + k} $$

答案： $0$

解 1：（来自 xxl）

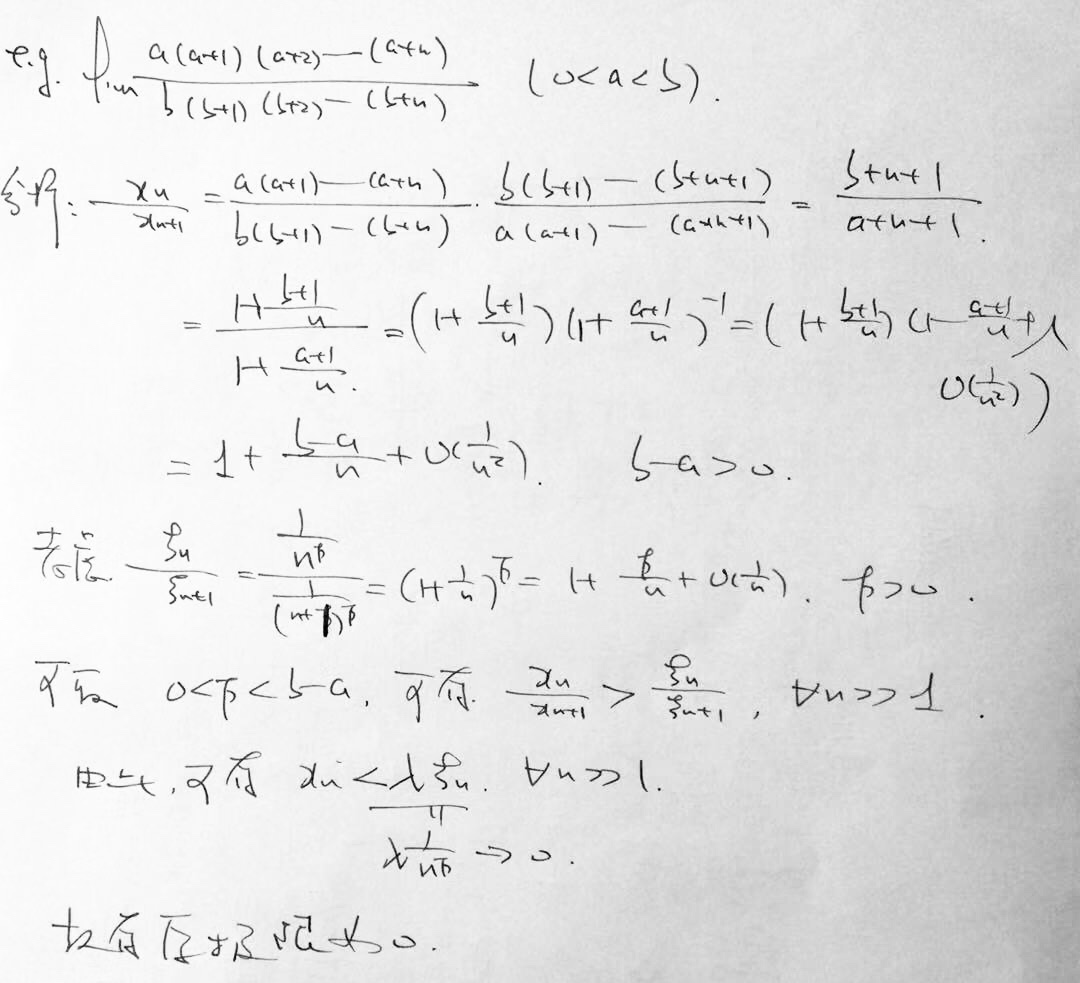
解 2： $\prod_{k = 0}^n (a + k) = \Gamma(n + a + 1) / \Gamma(a)$，再利用 Stirling 近似暴力分析。

$$ \Gamma(n + 1) = \sqrt{2\pi n}\left({n \over \mathrm e}\right)^n\color{silver}\left(1 + \mathrm O\left(\frac1n\right)\right) $$

斯特林近似公式