浅谈扩展 Thomae 函数的可微性

一般定义的 Thomae’s Function $f(x)$ 为：

$$ f(x) = \begin{cases} 1/p & x \in \mathbb Q,\ x = q/p,\ p \in \mathbb N^+,\ q \in \mathbb Z,\ p \bot q \\ 0 & x \in \mathbb R \backslash \mathbb Q \end{cases} $$

有时也被称为 Riemann 函数、爆米花函数。这个函数的一大特点就是它是一个周期为 $1$ 的函数（证明非常简单），所以研究时只需要考虑 $[0,\ 1)$ 内的情况就好了。下文分析时都假定 $0 \leqslant x < 1$。扩展的 Thomae 函数主要修改了有理点的取值：

$$ f_k(x) = \begin{cases} 1/p^k & x \in \mathbb Q,\ x = q/p,\ p \in \mathbb N^+,\ q \in \mathbb Z,\ p \bot q \\ 0 & x \in \mathbb R \backslash \mathbb Q \end{cases} $$

显然 $f_1$ 就是原来的函数。随着次数的增大，整个函数的图像也会越来越贴近 $x$ 轴：

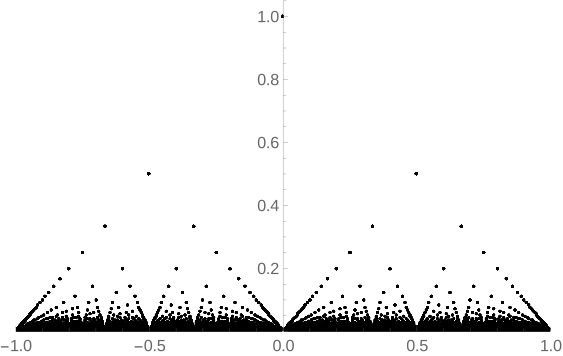
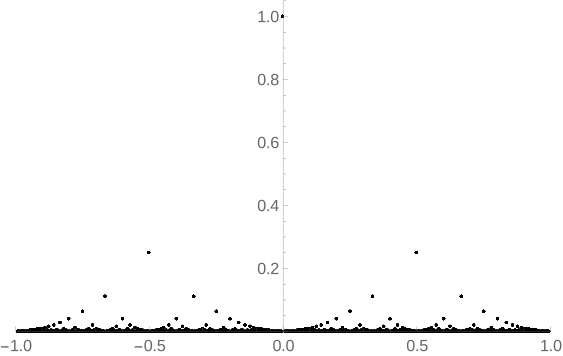
连续性

首先看一下这个函数在每个点的函数极限 $\lim_{x \rightarrow x_0} f_k(x)$，凭直觉来讲应该是 $0$。直接采用函数极限的 $\varepsilon$-$\delta$ 定义，对于所有 $1/p^k \geqslant \varepsilon$ 的 $p$，把 $(0,\ 1)$ 内以 $p$ 为分母的分数全部拿出来，最后得到 $\{1/2,\ 1/3,\ 2/3,\ ...\}$。这样的分数是有限个的，所以可以将它们按大小排序。如果 $x_0$ 是有理数且也在其中，则将 $x_0$ 删去，毕竟 $f_k(x_0)$ 是多少对函数极限来讲并不重要。然后以这些有理点对区间 $[0,\ 1)$ 进行切割，这时 $x_0$ 必在某个小区间 $(l,\ r)$ 中，对于任意的 $x \in (l,\ r)$，显然有 $f_k(x) < \varepsilon$，所以可以得知函数极限为 $0$。

这样一来，不难得出 $f_k(x)$ 在无理点连续，有理点不连续的结论了。换句话说，$f_k(x)$ 不可能在有理点可微。故接下来就不再考虑有理点了。

$f_1(x)$ 的可微性

对于一元函数，可导和可微是等价的。在 $a$ 处可导的定义就是下面这个极限：

$$ \lim_{x\rightarrow a} {f_1(x) - f_1(a) \over x - a} \xlongequal{a \text{ irrational}} \lim_{x \rightarrow a} {f_1(x) \over x - a} $$

存在。稍作尝试估计都会觉得不存在。首先，假设这个极限存在，那么对于任意趋近于 $a$ 的无理数列 $x_n$，显然：

$$ \lim {f_1(x_n) \over x_n - a} = 0 $$

那么其导数必然为 $0$。从另外一个角度也可以说明这一点：这需要我们注意到所有的无理点都是 $f_k(x)$ 的极小值点，在假设 $a$ 处可微的情况下，根据 Fermat 引理，可以知道 $a$ 是一个驻点。

为了证明极限不存在，我们需要再构造一个趋近于 $a$ 的实数列 $y_n$，使得类似的极限不为 $0$。考虑构造一个有理数列？首先，所谓趋近于 $a$ 就是对任意小的 $\varepsilon > 0$，从某一项开始都有 $|y_n - a| < \varepsilon$。设 $y_n = q/p > a$，那么不难得知 $f_1(y_n) \geqslant 1/p$¹。考虑极限：

$$ \lim {1/p \over q/p - a} \leqslant \lim {f_1(y_n) \over q/p - a} $$

如果 $0 < q/p - a \leqslant 1/p$，那么若其有极限，则极限至少不小于 $1$，我们的目的就达成了。我们总能找到这样的 $p$，满足 $1/p < \varepsilon$，这样一来 $y_n - a \leqslant 1/p < \varepsilon$。同时，$q$ 只需要满足 $ap < q \leqslant ap + 1$。令 $q = \lceil ap \rceil$ 就 OK 了。于是我们就构造出了预期的有理数列。所以 $f_1(x)$ 处处不可导，同时也处处不可微。

$f_2(x)$ 的可微性

初步尝试

对于 $f_2(x)$ 尝试下同样的方法：构造趋近于无理数 $a$ 的有理数列 $\{x_n\}$，使得：

$$ \lim {f_2(x_n) \over x_n - a} $$

不等于 $0$。设 $x_n = q/p$，那么 $f_2(x_n) \geqslant 1/p^2$。为了方便处理，令 $x_n = q/p > a$，那么：

$$ {1/p^2 \over q/p - a} \geqslant 1 \iff ap < q \leqslant ap + 1/p $$

显然如果这样的 $q$ 存在，$q$ 只能为 $\lceil ap \rceil$。但麻烦的一点在于，上面这个不等式构成的区间长度仅有 $1/p$，不能直接保证 $q$ 就在其中 QAQ

Dirichlet 定理

现在的麻烦在于确定：

$$ q \leqslant ap + \frac1p \iff ap - q + \frac1p \geqslant 0 $$

是否总是有解 $p$ 和 $q$，而且 $p$ 可以取得非常大，才能满足 $x_n$ 趋向 $a$ 的目标。考虑到 $ap - \lceil ap \rceil = \{ap\} - 1 < 0$²，于是变为：

$$ \{ap\} \geqslant 1 - \frac1p = \frac{p-1}p \tag{1} $$

不难想象，如果 $a$ 是有理数，这个不等式在 $p$ 很大的情况是肯定会 fail 的。不过现在 $a$ 是无理数。直接处理起来有点棘手，但我们可以尝试有理数近似无理数的思想。这里我们利用 Dirichlet 近似定理（Dirichlet’s Approximation Theorem）：

设 $\alpha$ 为实数，对于任意正整数 $n$，总存在整数 $q$ 和 $[1,\ n]$ 内的正整数 $p$，满足：
$$ |p\alpha - q| < \frac1n $$

也就是：
$$ \left|\alpha - \frac{q}p\right| < \frac1{np} \leqslant \frac1{p^2} $$

虽然说还有更强的结论，但 Dirichlet 近似定理给人的感觉已经足够厉害并且形式简单。它的证明也相当初等：只需要用到鸽巢原理。直观上理解，$|p\alpha - q|$ 这个东西的最小值就是 $\min\{\{p\alpha\},\ 1 - \{p\alpha\}\}$，因此目标就是证明存在 $p \leqslant n$ 使得这个东西小于 $1/n$。如果存在 $p$ 使得 $\{p\alpha\}$ 小于 $1/n$ 或者大于 $1 - 1/n$，那么结论直接成立。那有可能没有吗？考虑 $\{0\cdot \alpha\}$、$\{1\cdot \alpha\}$、…、$\{n\alpha\}$ 一共 $n + 1$ 个值，同时将区间 $[0,\ 1)$ $n$ 等分为 $[0,\ 1/n)$、$[1/n,\ 2/n)$、…、$[(n-1)/n,\ 1)$，根据鸽巢原理，必定存在 $0 \leqslant i < j \leqslant n$，使得 $\{i\alpha\}$ 和 $\{j\alpha\}$ 在同一个区间里面。于是乎：

$$ |\{j\alpha\} - \{i\alpha\}| < 1/n \tag{2} $$

这时把整数部分补上就可以完成证明：令 $p = j - i \in [1,\ n]$，$q = \lfloor j\alpha \rfloor - \lfloor i\alpha \rfloor \in \mathbb Z$，那么 $|p\alpha - q|$ 就变成了 $(2)$ 中的式子，定理证明完毕。

当 $p > 1$ 时，$1/p^2$ 显然小于 $1/p$，而相邻两个 $q/p$ 的差却为 $1/p$，所以对于特定的 $p$，满足条件的 $q$ 是唯一的。当然特殊情况 $p = 1$ 时，也只有 $\alpha = 1/2 + k \:\: (k \in \mathbb Z)$ 时才能有两个 $q$，不过可惜 $\alpha$ 为无理数，所以无论哪种情况都可以视作唯一的。从这一点可以得到 Dirichlet 近似定理的一个推论：

推论 1　设 $\alpha$ 为无理数³，存在无穷多的 $q$ 和 $p$（$q$ 是整数，$p$ 是正整数）满足：
$$ \left|\alpha - \frac{q}p\right| < \frac1{p^2} $$

证明　假设这种近似数量有限，设为 $q_1/p_1,\ q_2/p_2,\ ...,\ q_m/p_m$，那么取足够大的 $n$ 使得 $1/n < \min|\alpha - p_k/q_k| \:\: (1 \leqslant k \leqslant m)$。由于 $\alpha$ 为无理数，所以不等式右边肯定不是 $0$。于是根据 Dirichlet 定理，必定能再得到 $q_{m + 1}/p_{m + 1}$ 满足 $|\alpha - q_{m + 1}/p_{m + 1}| < 1/np_{m + 1} \leqslant 1/n$，这表明新的近似比之前的近似都更加优秀，不可能在前 $m$ 个中出现过，与假设相矛盾。

考虑到 $q$ 的唯一性，上述定理还可以写做：

推论 2　设 $\alpha$ 为无理数，存在无穷多的正整数 $n$ 满足：
$$ \min\{\{n\alpha\},\ 1 - \{n\alpha\}\} < \frac1n \tag{3} $$

最后一步

现在是时候回到正题，因为我们已经发觉 $(3)$ 式与 $(1)$ 式的高度相似性了：

$$ \{ap\} \geqslant 1 - \frac1p \iff 1 - \{ap\} \leqslant \frac1p \tag{1} $$

But…我们并没有充足的理由说最小值一定就总是能取到 $1 - \{n\alpha\}$ 这一边。如果总取到另外一边就 GG 了。虽然有结论表明 $n\alpha$ 的小数部分是在 $(0,\ 1)$ 上均匀分布的⁴，但为了使分析尽可能初等，我们不得不对之前 $f_2(x)$ 在 $a$ 处的导数极限做一些更加精细的分析。在之前为了方便，我们假定了 $x_n > a$。现在放开这条限制，允许 $x_n < a$，不过这时 $f_2(x) / (x_n - a)$ 就变成负数了。直觉上我们希望：

$$ {f_2(x) \over x_n - a} \leqslant {1/p^2 \over q/p - a} \leqslant -1 $$

这时可以推出：

$$ ap - \frac1p \leqslant q < ap $$

所以 $q$ 只能为 $\lfloor ap \rfloor$。由于 $ap - q = ap - \lfloor ap \rfloor = \{ap\}$，所以得到 $p$ 只需要满足 $\{ap\} \leqslant 1/p$。换言之，在不等式 $(3)$ 中，我们先可以取足够大的 $p$，使得 $\varepsilon > 1/p$ 以满足函数极限逼近的要求，然后考虑 $\min$ 的取值。若是取到左边，则存在 $q = \lfloor ap \rfloor$ 使得 $f_2(x) / (x_n - a) \leqslant -1$。反之 $q = \lceil ap \rceil$ 使得这个东西不小于 $1$。这样无论如何，极限要么不存在，要么就不等于 $0$。所以 $f_2(x)$ 在 $a$ 处不可微。

综上 $f_1(x)$ 和 $f_2(x)$ 都是处处不可微的。

$f_3(x)$ 的可微性

对于 $f_3(x)$，Dirichlet 近似定理的结论已经不够用了，继续下去可能需要动用无理测度的理论，如参考资料 [BRS09] 所用的方法。我太菜了不懂这套理论，只能就此打住了。实际上，在这个参考资料里已经证明了：$f_3(x)$ 有可微点。

但是，无论 $f_k(x)$ 的 $k$ 有多大，这个函数总是有许多不可微的无理点。为了得到这一点，我们可以利用一个闭区间套 $\{[l_i,\ r_i]\}$ 来辅助构造一个极限为无理数的有理数列 $x_i \in [l_i,\ r_i]$。这个构造的关键在于有理数集是可数的，所以可以用一个数列 $a_i$ 来映射所有有理数。初始时，随意取一个闭区间 $[l_1,\ r_1]$，然后尝试将有理数 $a_1$ 从这个区间中切掉：如果 $a_1 \notin [l_1,\ r_1]$，无需做任何操作；否则取一个足够小的 $\varepsilon$，然后选取 $[l_1,\ a_1 - \varepsilon]$ 或 $[a_1 + \varepsilon,\ r_1]$ 为闭区间套的下一个区间。之后的操作与之类似。此外，通过适当缩短区间使得闭区间的长度收敛于 $0$（具体而言，可以在构造过程中让 $[l_i,\ r_i]$ 交上 $[l_i,\ l_i + 1/i]$ 来作为第 $i$ 个闭区间）。这样 $x_i$ 就会收敛于某个数 $a$。如果 $a \in \mathbb Q$，那么存在 $i \in \mathbb N^+$，有 $a_i = a$。而 $a_i \notin [l_i,\ r_i]$，$\lim x_i \in [l_i,\ r_i]$，这就产生了矛盾。所以 $a$ 必须为无理数⁵。

我们可以在构造过程中加入更多的限制，例如，对于可微性相当致命的条件莫过于 $|f_k(x) / (x - a)| \geqslant 1$ 了（之前一直都是在配合它来证明的处处不可微）。所以构造步骤中再加上 $[l_i,\ r_i]$ 与 $[x_i - f_k(x_i),\ x_i + f_k(x_i)]$ 求交，这样 $\lim f(x_i) / (x_i - a)$ 就无法收敛于 $0$ 了。同理，设 $f_k(x)$ 的不可微无理点构成集合 $A$，如果 $A$ 是可列集，那么可以像对待有理数集 $\mathbb Q$ 一样，在构造中将其依次挖去，最后得到集合 $A$ 之外的一个不可微无理点，这就产生了矛盾，从而证明 $A$ 甚至是不可数的！总而言之，Thomae 函数想让每个无理点都可微是根本就不可能的啦 0.0⁶

参考资料

[DAP]. “Dirichlet’s Approximation Theorem“
[BRS09]. Kevin Beanland, James W. Roberts, Craig Stevenson, “Modifications of Thomae’s Function and Differentiability” (2009), The Mathematical Association of America Monthly 116
[AoPS]. “Rational approximation”, Art of Problem Solving Wiki