Hall 定理

基本形式

Hall 定理是一个用于判定二分图是否具有完美匹配的定理。
首先对于二分图 $G = (X \cup Y, E)$，点集被分为了 $X$ 和 $Y$ 两部分。
是否具有完美匹配，首先一个最基本的条件就是 $|X| = |Y|$。
Hall 定理则在此基础上给出了一个更强的条件。
首先对于一个点集 $T \subseteq X$，定义 $\Gamma(T)$ 如下：
$$ \Gamma(T) = \{v \mid u \rightarrow v \in E,\; u \in T,\; v \in Y\} $$

即表示 $T$ 中所有点能够直接到达的 $Y$ 中的点的集合。

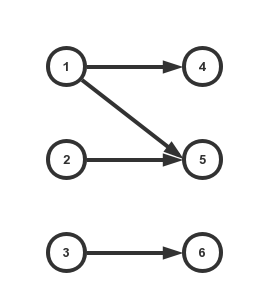
bigraph

上图中，$\Gamma(\{1,\;3\}) = \{4,\;5,\;6\}$。
Hall 条件用于判断一个二分图是否存在完美匹配。如果对于任意的点集 $T \subseteq X$，均存在：
$$ |T| \le |\Gamma(T)| $$

称此二分图满足 Hall 条件。Hall 定理的表述如下：

二分图 $G(X \cup Y,E)$ 存在完美匹配当且仅当 $|X| = |Y|$ 并且满足 Hall 条件。

本文会使用 $C = A - B$ 表示集合之差，即 $C = A \cap \overline B$。

证明

首先，当 $|X| \neq |Y|$ 时，二分图不存在完美匹配。如果二分图存在完美匹配，则意味着 $|X| = |Y|$。此外，上述定理的充分性非常显然，因为如果 $|\Gamma(T)| < |T|$，那么对于子集 $T$ 是无法找出完美匹配的。

现在来证明必要性。记 $n = |X|$，不难发现当 $n = 0$ 或 $n = 1$ 时，Hall 定理是成立的。

尝试使用数学归纳法来证明 $n > 1$ 的情形。假设对于任意 $n < k$ 的情况都是成立的，则需要证明当 $n = k$ 时也是成立的。先来考虑条件最为苛刻的一类非空真子集 $T \subset X$，它满足 $|\Gamma(T)| = |T|$。对于子集 $S \subseteq X - T$，由于满足 Hall 条件，所以 $|\Gamma(S \cap T)| \geq |S \cap T|$，又因为 $|\Gamma(T)| = |T|$，所以 $|\Gamma(S) - \Gamma(T)| \geq |S|$，也就是说，如果图 $G$ 中删去 $T$ 和 $\Gamma(T)$ 中的所有点得到新图 $G'(X' \cup Y',E')$，则 $|X'| < k$ 且依然满足 Hall 条件，故 $G'$ 存在完美匹配。由于 $T$ 是真子集，所以 $|T| < k$，所以 $G$ 关于点集 $T \cup \Gamma(T)$ 的导出子图一定存在完美匹配。即 $G$ 存在完美匹配。

注意到满足上述条件的非空真子集 $T$ 并不总是存在。当不存在的时候，我们有：
$$ |\Gamma(T)| \geq |T| + 1 \;\;\;\; (\forall \; T \subset X) $$

这个时候任意删去图 $G$ 的任意一条匹配边，不会使 $G$ 不符合 Hall 条件。由于 $n$ 减少了 $1$，所以删去该匹配边后的图存在完美匹配。

计算所有满足 Hall 条件的子集

对于一张二分图而言，如何确定 $X$ 或 $Y$ 的一个子集是否满足 Hall 条件？
令 $n$ 为 $|X|$。首先我们可以根据定义，对于每个子集枚举自己的子集。采用 DP，可以推算出所有子集的答案。时间复杂度为 $O(3^n)$。
考虑到直接枚举子集过于暴力，因此先选择集合中的一个点 $u$，将其删去，将会得到一个更小的子集，这个值已经被提前计算过了，因此一大部分的子集的答案就都被算入其中了。剩下的还未考虑到的子集均包含 $u$，但是除了集合本身外，剩余的子集均会相差至少一个点。因此我们枚举所有集合中的点并去掉，用得到的新的更小的集合的 DP 值来更新当前集合，最后再计算自己是否满足不等式。这样计算的时间是 $O(2^n \cdot n)$ 的。

大致的代码如下：

f = [True] * 2^n  // DP数组
for s in [0, 2^n):
    for u in [0, n):
        f[s] &= f[s ^ (1 << u)]
    # 检查s本身是否可行，更新f[s]

简单运用

Hall 定理一般没有什么优化算法复杂度上的用途，但是可以作为一个比较好的思维工具。
例如下面这个问题：
[Russian Code Cup 2016 - Finals] A. Closing ceremony

大意是有一个 $n\times m$ 的网格和 $n \times m$ 个人，每个人都要走到一个网格上的一点，每个点只能装下一个人。
同时定义两个点之间的距离为曼哈顿距离，每个人有自己行走的路程上限。
现在这 $n \times m$ 个人分成两批，从 $(0,\;0)$ 和 $(0,\;m+1)$ 出发，问你是否存在一种安排每个人的最终位置的方案，来满足每个人走到对应位置时的路程不超过自己的上限。

令点 $A$ 为 $(0,\;0)$，点 $B$ 为 $(0,\;m+1)$。并且设 $f(i,\;j)$ 表示离 $A$ 距离至少为 $i$，离 $B$ 距离至少为 $j$ 的格子的个数。
设 $S_A(i)$ 表示在 $A$ 最远距离至少为 $i$ 的人数，同理，$S_B(i)$ 表示在 $B$ 处最远距离至少为 $i$ 的人数。由于每个人和一个位置形成了一个一一对应的关系，由此我们可以构建一个二分图，并且我们所要做的就是判定这个二分图是否具有完美匹配。
事实上由于存在单调性，利用 Hall 定理可以知道，我们只用判定是否对于所有的 $f(i,\;j)$ 均不大于 $S_A(i) + S_B(j)$，如果满足这个条件，那么这个二分图就有最大匹配。
那么现在的问题就是求得 $f$。由于曼哈顿距离为 $i$ 的等距线实际上是一条斜率为 $1$ 或 $-1$ 的直线，所以 $f(i,\;j)$ 就是两条直线在网格中围成的面积。
并且注意到它可以递归计算：
$$ f(i,\;j) = f(i+1,\;j) + f(i,\;j+1) - f(i+1,\;j+1) $$

并且需要考虑这两条直线的交点是否会占用一个格子。所以我们的做法就是枚举交点，确定是那两条直线相交，并且赋给对应的 $f$ 去，然后对 $f$ 计算后缀和就是我们想要的东西啦～