树状数组

树状数组是一种快速统计前缀和的简单数据结构。

基本问题

很多情况下，我们需要查询区间内的和，通常万能的做法就是线段。写过线段树的都知道，它其实并不简单，当然也不太难。而有了树状数组后，就可以以比线段树少很多代码，来统计区间和。

区间求和的问题一般是这样的：

给你一个长度为$n$的数列，然后每次给你一个区间询问，询问这段区间内数的总和。

求区间和可以通过求前缀和而得。即查询$S[l, r]$可以转变为$S[1, R] - S[1, L - 1]$。其中$S$表示区间和。

点修改区间查询

我们将先看到几个特化过的区间求和问题。树状数组的最基本用场就是点修改 + 区间查询了。它要求支持两个操作：

修改某一位置上的数
查询某一位置前缀和

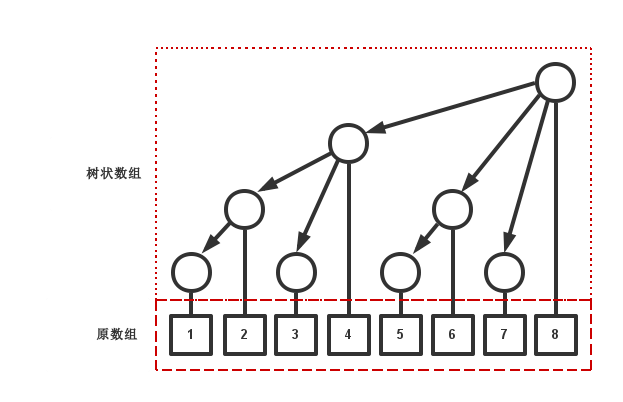
fenwick

树状数组是套在原数组上的一层²，用来进行一些维护。上图中的树状数组被画成了它该有的样子，实际上就是一个数组。
对于数组中的每一个元素，其箭头所指向的元素(包括他自己)都被它所维护。
对于任意一个元素，其往前的一个区间距离和到它父亲的距离是相同的，即一个被称为$\text{lowbit}$的东西。这个东西定义如下：

1 2	function LOWBIT(x): return x & (-x)

这里面用到一个很玄乎的位运算，至于为什么是这样，这里就不多说了。
对于LOWBIT有一个需要注意的地方，就是LOWBIT(0) = 0。即树状数组不能处理下标为$0$的情况¹。如果不注意，就很容易出现死循环。

对于每次单点的更新，我们都要将它的父亲给更新，因为它是被其父亲所管辖的。
而查询可以向前进行统计，这样就可统计前缀和。

下面用fenwick表示树状数组，n表示其长度。

// 修改单点
function MODIFY(x, delta):
    if x < 1:
        return

    while x <= n:
        fenwick[x] += delta
        x += LOWBIT(x)

// 查询前缀和
function QUERY(right):
    answer = 0

    while right > 0:
        answer += fenwick[right]
        right -= LOWBIT(right)

    return answer

对于每个操作，其中的循环只要进行$\Theta(\log n)$次，故它们的时间复杂度为$\Theta(\log n)$的。

区间修改点查询

对于区间修改 + 点查询的问题通常要支持一下两种操作：

修改一段前缀和
查询某一个位置上数的大小

fenwick

考虑到能够影响到一个点的值的，只有其父亲。因此每次修改前缀和时，只需要修改它们的某一个父亲即可。查询单点时，也只需要访问其每一个父亲，从而可以得知自己被加上了多少。

// 修改
function MODIFY(right, delta):
    while right > 0:
        fenwick[right] += delta
        right -= LOWBIT(right)

// 查询
function QUERY(x):
    if x < 1:
        return 0

    answer = 0

    while x <= n:
        answer += fenwick[x]
        x += LOWBIT(x)

    return answer

与前面一样，这两个操作的时间复杂度也是$\Theta(\log n)$。

区间修改区间查询

事实上，上面两种特化版本并不是太常见，最常见的因该是完整的区间和问题。对于这个问题，我们只要实现一下两种操作：

修改一段前缀和
查询一段前缀和

由于树状数组的一些特殊性，它的查询不是从所谓的根节点开始的，因此在父亲信息都会丢失掉。然而要将他们统计回来时，却需要很高的代价。因此一个树状数组不好解决这个问题。
所以我们同时使用两个树状数组，一个用于查询其儿子们的信息，另外一个则用于查询父亲的信息。

具体实现时，我们使用fenwick1来记录其父亲的信息，fenwick1[x]表示的是前x个数每个都被加上的数。使用fenwick2来记录儿子的信息，fenwick2[x]表示的是第x个元素所管辖的范围内的元素之和。这样对两个数组都查询一次，就可以得到完整的信息。

// 修改
function MODIFY(right, delta):
    if right < 1:
        return

    i = right
    while i > 0:
        fenwick1[i] += delta
        i -= LOWBIT(i)
    i = right
    while i <= n:
        fenwick2[i] += delta * right  // 注意是区间每一个数都加上了delta
        i += LOWBIT(i)

function QUERY(right):
    if right < 1:
        return 0

    answer = 0

    i = right
    while i <= n:  // 统计父亲上的信息
        answer += fenwick1[i]
        i += LOWBIT(i)
    answer *= right  // 因为是每个数所加上的数，所以要乘以个数

    i = right - 1
    while i > 0:  // 统计儿子信息
        answer += fenwick2[i]
        i -= LOWBIT(i)

    return answer

按照国际惯例，时间复杂度依然保持在$\Theta(\log n)$。

更高维度

有时候我们需要对二维或三维上进行求和，线段树当然可以做，只是代码量将以$O(2^k)$的复杂度暴涨，并且巨大的常数也难以接受。但此时树状数组却可以很好的因对。
那是因为每一个树状数组的的最后一个元素实际管辖的是整个数列的和，因此我们可以将它单独挑出来代表这一个数列。当我们有很多个数列时，我们将这些代表也用一个树状数组来维护。这样就实现了树状数组向高维度的扩展。

具体实现方面就是在每个操作中多了几层循环，用于在每一个维度中的统计。最后要得知一段区间中的和时，利用容斥原理即可。

由于在每一维上都需要花费$\Theta(\log n)$的时间，因此对于$k$为空间的操作的复杂度一般都是$\Theta(\log^k n)$。

优势与缺点

树状数组有着很多的优点：

代码短小，常数小
易于调试
容易扩展到高维度的数据

也正因为如此，树状数组也有着许多的局限性：

只能用于求和³，不能求最大/小值
不能动态插入，面多多维数据时空间压力大
不能可持久化

因此，在树状数组与线段树中进行抉择时，是需要小心的。树状数组虽好，但不是万能的。要根据实际情况来确定。

如果下标一定要为$0$，可以考虑将其全部加$1$。 ↩
当然也可以直接替代原数组。 ↩
或者说具有区间减法性质的数据。 ↩