排列与组合

排列与组合是组合数学中最基础的东西了。在此做一点记录。

阶乘

在组合数学中，阶乘随处可见，它极大的简化了公式的形式。
我们将$n!$记作$n$的阶乘，其定义如下：
$n! = \prod^n_{i=1} i \tag{1.1}$

特别的，$0! = 1$。之所以$0$的阶乘这样定义，是为了使后面的公式更具有普遍性。

我们来看一下阶乘函数的增长：

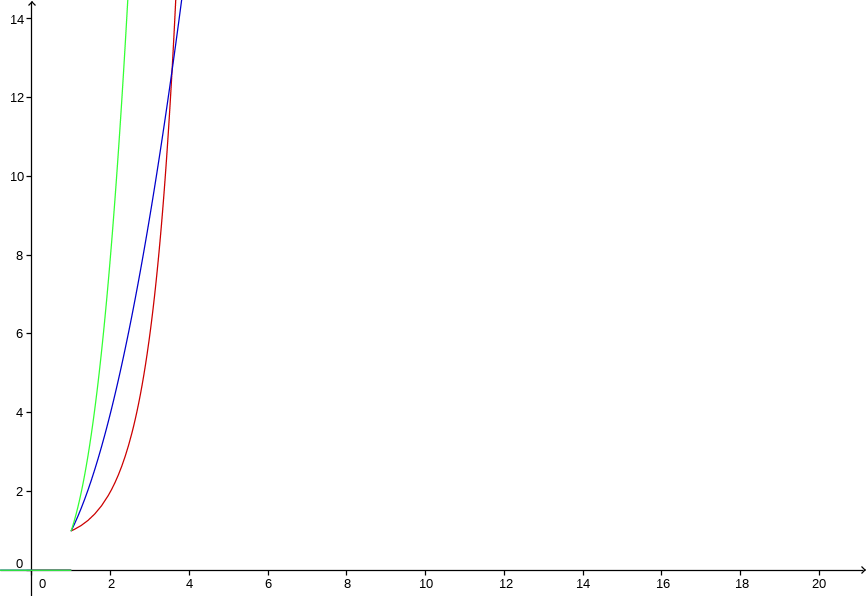
上图中，红色的阶乘函数$f(x) = x!$，蓝色的是$g(x) = x^2$，而绿色的是$h(x) = x^3$。
由此可见阶乘函数的增长比平方快。与三次方相比，阶乘函数在之后也将赶超。
因此如果时间复杂度里面出现了阶乘，那将是一件可怕的事情。

排列

对于一个集合$S$，其排列是$S$中的元素的有序放置。
例如集合$S = \{ a, b, c \}$，它的1排列为：
$a, b, c$

其2排列为：
$ab, ac, ba, bc, ca, cb$

3排列为：
$abc, acb, bac, bca, cab, cba$

由于$|S| < 4$，所以$S$没有4排列。

为了方便计数，我们将一个含有$n$个元素的集合的$r$排列个数记为$P(n, r)$¹。
如：$P(3,1)=3, \; P(3,2)=P(3,3)=6$。
特别的，我们定义$P(n,0)=1$。

如何计算这个值呢？当然我们是有公式的：
定理 对于任意的$n, r \in N_+$，并且$r \le n$，有：
$P(n, r) = {n! \over (n-r)!} \tag{2.1}$

证明 我们有$r$个空位来摆放元素。在第一个空位我们有$n$种选择，在第二个空位我们有$n - 1$中选择......由此可以得知：
$P(n, r) = \prod^n_{i=n-r+1} i = {n! \over (n-r)!}$

现在我们来运用一下排列。
首先来计数由$1$至$9$的数构成的每一位均不同的$7$位数有多少个。
这个非常简单，就是$P(9, 7) = 181440$。

如果现在要求$5$和$6$不能连续出现，那么这样的数又有多少个？
我们考虑将连续出现的数给计数出来，这样就可以得到答案。
我们发现，通过向一个$5$位数中插入两个数就可以得到一个$7$位数，因此我们来考虑将$5$和$6$连续的插入一个$5$位数中。我们只会插入$56$或$65$，它们在一个$5$位数中一共有$6$个位置可以插入。因此$5$和$6$连续出现的数共有$2 \times 6 \times P(7, 5) = 30240$个。
因此最终的答案为$181440 - 30240 = 151200$。

组合

与排列相对，一个集合的组合²是其元素的无序放置。
其含义就是从集合中”选取”出几个元素。由于不考虑位置关系，所以像$abc$和$bac$³是等价的。

组合这一概念在整个组合数学中用处十分巨大。接下来我们先看到如何计数它。
首先我们将组合数记为${n \choose r}$⁴，表示一个大小为$n$的集合的$r$组合的个数。例如，一个大小为$4$的集合$S = \{ a,b,c,d\}$的3组合为：
$\{a,b,c\}, \{a,b,d\}, \{a,c,d\}, \{b,c,d\}$

因此${4 \choose 3} = 4$。

同样，为了能够更加方便的计数它，我们当然也是有公式的。
我们发现，任意一个$r$组合，都会有$P(r,r) = r!$种排列。而每一种排列，都会对应到一个组合。因此，一个集合的$r$组合与排列之间存在以下关系：
${n \choose r}r! = P(n,r) \tag{3.1}$

将排列数展开，我们可以得到下面的公式：
${n \choose r} = {n! \over (n-r)!r! } \tag{3.2}$

其中，$n,r \in N_+$，且$r\le n$。

组合数的基本性质

组合数有着许多非常有用的性质。首先一个非常基本的等式就是：
${n \choose r} = {n \choose n-r} \tag{4.1}$

直接利用组合数的公式可以得证这一性质。

通过对组合数进行求和，我们可以得知一个集合的子集数量：
$\sum^n_{i=0} {n\choose i} = 2^n \tag{4.2}$

这个等式当然可以用求和来得出。我们可以换个角度来考量它。一个集合的子集中，某些元素要么没有出现，要么就出现了。因此对于每个元素一共有两种选择，因此子集的总数为$2^n$个。

接下来是比较重要的帕斯卡公式：
定理 对于所有的$1 \le k \le n-1$的整数$n$和$k$：
${n\choose k} = {n-1\choose k} + {n-1\choose k-1} \tag{4.3}$

证明 尝试将右式化为左式即可。
$\begin{aligned} {n-1\choose k} + {n-1\choose k-1} &= {(n-1)! \over k!(n-k-1)!} + {(n-1)! \over (k-1)!(n-k)!} \\ &= {(n-1)!(n-k) \over k!(n-k)!} + {(n-1)!k \over k!(n-k)!} \\ &= {(n-1)!n \over k!(n-k)!} \\ &= {n! \over k!(n-k)!} \\ &= {n \choose k} \end{aligned}$

这样就完成了证明。注意，在上面的证明中，利用到了阶乘的性质：$(n-1)!\cdot n=n!$。

不难发现，帕斯卡公式实际上是组合数的一个递推公式。

上图是由帕斯卡公式得到的一个递推的关系图，这里以${4 \choose 3}$为例。其中灰色的节点是无效的值。为了方便，直接将其设为$0$。除了${1 \choose 0} = {1 \choose 1} = 1$为初始值外，其它的值都是由其所指向的节点的值求和而来。
上面的步骤就是动态规划中的状态转移的过程。利用这个公式，我们可以在$\Theta(nr)$的时间来计算大量的组合数。因此可以将此作为一个预处理。
在具体实现的时候只需注意一些无效的特殊情况，其中包括$r > n$和$n < 0$或$r < 0$。这些情况下的值均设为$0$。然后通过${1 \choose 0}$和${1 \choose 1}$这两个初始值就可以完成递推。