树链剖分

用途

问题: 给你一棵无根树，每条边有边权，请你实现以下操作：

查询$u$到$v$的路径上边权之和。
查询$u$到$v$的路径上边权最大值。
修改$u$到$v$的路径上每条边的边权。
…

这些操作利用树链剖分，都可以在$O(\log n)$的时间内解决。

无根树与有根树

一般来说，无根树是很不好处理的，因此将其转为有根树就会好处理些。
我们只要选定一个节点为根，然后进行DFS即可转化为有根树。

转换的时候，我们需要额外记录以下信息：

$x.\text{father}$: $x$的父亲节点。
$x.\text{children}$: $x$的所有孩子。
$x.\text{size}$: 以$x$为根的这一棵子树的大小。
$x.\text{depth}$: $x$在树中的深度，即$x$到树根的距离$+1$。

tree-normal
这是一棵以$1$为根的树。为了解释更加清楚，这里举几个例子：

$10.\text{father} = 5,\; 1.\text{father} = nil$
$1.\text{children} = \{2, 5, 6\},\;7.\text{children} = \varnothing$
$1.\text{size} = 17,\;6.\text{size} = 8,\;3.\text{size} = 1$
$1.\text{depth} = 1,\;10.\text{depth} = 3,\;14.\text{depth} = 4$

为了进行树链剖分，我们在立树的过程中需要计算一个重儿子，记作$x.\text{next}$：
$$ x.\text{next} = u: u \in x.\text{children},\;u.\text{size}\text{最大} $$

即所有儿子中大小最大的一个，就记为重儿子，其它的儿子就是轻儿子。同时称与重儿子相连的边为重边，与轻儿子相连的边为轻边。

下面的伪代码是建立有根树的过程(假设我们输入的是无根树$G$，这是一张无向图，其中与$u$相连的顶点集合为$G[u].\text{neighbors}$)：

function MAKE-ROOT(G, u):  // 以u为树根
    u.visited = true  // u已经访问过了
    u.father = nil // u没有父亲
    u.depth = 1

    REAL-MAKE-ROOT(G, u)

function REAL-MAKE-ROOT(G, u):  // DFS过程
    u.size = 1
    u.next = nil

    foreach v in G[u].neighbors:
        if not v.visited:  // 如果还未访问
            v.visited = true
            u.children += v  // 添加儿子节点
            v.father = u
            v.depth = u.depth + 1

            REAL-MAKE-ROOT(G, v)  // 递归向下

            u.size += v.size  // 更新子树大小

            if u.next = nil || v.size > u.next.size:  // 更新重儿子
                u.next = v

剖分

在介绍树链剖分的算法之前，我们先来看看剖分后的树是个什么样子：
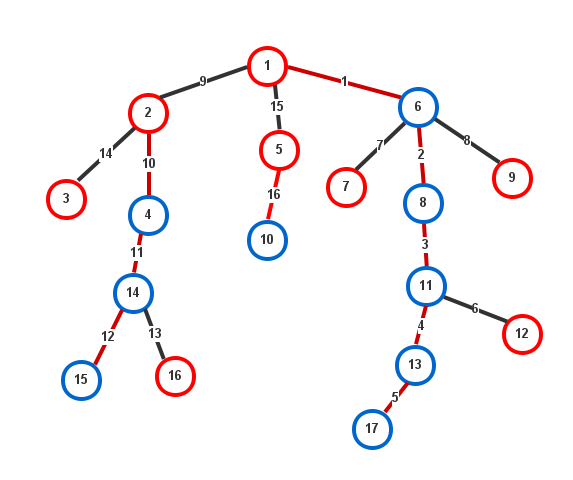
tree-splited
剖分后的树信息量一下子大了很多。我将会逐条解释上面都画了些什么。

树链(重链): 所有红色的边所连成的一条链都是剖分后的结果。某些树链没有边，就只有一个节点，这个节点是红色的。在上面，1-6-8-11-13-17是剖分出来的最长的树链，而3独自一个节点形成了树链。
树链起点: 红色的节点是每一条树链的起点。
重儿子: 蓝色的节点是重儿子。
编号: 每一条边上的数字为剖分后的编号。

可以看出，树中的每一个节点都会在一条树链中。因此我们需要对树链也进行编号。我们以树链顶端的节点作为树链的编号，并记为$x.\text{top}$。例如，$8.\text{top} = 1,\;16.\text{top} = 16$。
如果两个节点$u$和$v$在同一树链中，当且仅当$u.\text{top} = v.\text{top}$。

对于边$u \rightarrow v$的编号，我们记边为二元组$(u, v)$，那么记编号为$(u,v).\text{id}$。
但是这样不方便在程序中储存，因此我们将边的编号放到节点里面。在上面的写法中，如果$u$是$v$的父亲，那么我们将边$(u,v)$的编号放到$v$中，即$v.\text{id}$。这样表示$v$与其父亲相连的边$(u,v)$的编号为$v.\text{id}$。

边的编号是树剖的关键，给边赋予编号后，就可以实现很多操作了。
我们首先来看这些编号有什么特点：

每个边的编号都不一样。
同一条的树链的边的编号从高处向低处编号递增。这样做的好处就是同一条链上面的数据可以用一些数据结构(如线段树、Splay等)来维护。
对于节点$u$，其重边的编号是$u$与所有儿子的连边中最小的。

估计你已经猜到计算$\text{top}$和$\text{id}$的用处了。但不要着急，下面就将计算这些值。

计算的过程也是一遍DFS。这次的DFS是在第一次建立好的有根树上进行的。
当我们处理到节点$u$时，我们将$u$和$u.\text{next}$相连来形成树链。之所以选取重儿子，是因为重儿子的大小最大，因此所生成的树链将尽可能长¹。那么其它的儿子将自己成为新的树链。
此时来考虑编号。因为同一条树链上的边的编号是递增的，因此要优先对重儿子进行DFS。由于轻儿子是新创建的树链，因此DFS的顺序并不重要。

至此，树链剖分的算法就结束了。当算法完成时，每个节点就会有正确的$\text{top}$和$\text{id}$。

下面是树链剖分的伪代码：

count = 0  // 已编号的数量

function TREE-SPLIT(x):  // 剖分子树u
    x.id = 0  // 根节点没有父亲
    x.top = x  // 根节点是第一条链

    REAL-TREE-SPLIT(x)

function REAL-TREE-SPLIT(x):  // DFS过程
    if x.next != nil:  // 如果有重儿子
        count += 1
        x.next.id = count
        x.next.top = x.top

        REAL-TREE-SPLIT(x.next)  // 优先重儿子

    foreach v in x.children:  // 对于轻儿子则新创一条链
        if v != x.next:  // 检查是不是重儿子
            count += 1
            v.id = count
            v.top = v

            REAL-TREE-SPLIT(v)

基础操作

树链剖分完有什么用呢？
就像一开场所说的：

查询$u$到$v$的路径上边权之和。
查询$u$到$v$的路径上边权最大值。
修改$u$到$v$的路径上每条边的边权。
…

下面将介绍如何进行路径边权之和的查询和修改路径边权这两个操作。其它的操作可以在此思想上扩展。

查询

假如我们要查询$u$到$v$的路径上的权值之和，那么就会有两种情况：

$u$和$v$在同一条树链上。
$u$和$v$不在同一条树链上。

对于第一种情况，非常好解决。我们可以用线段树来维护每一条边的权值，直接按照编号来排列。由于同一条链上的编号是递增的，如果$u.\text{depth} < v.\text{depth}$，则可以直接查询$[u.\text{next}.\text{id}, v.\text{id}]$的和。如果$u.\text{depth} = v.\text{depth}$，由于$u$和$v$是在同一条树链上的，也就是意味着$u = v$，那么就不需要统计。

对于第二种情况，我们考虑使它们不断逼近到同一条链上来，从而就转为了第一种情况。但是，在其中一个节点变化到另一条树链上时，要将经过的树链的值进行统计。
我们按照一下步骤来处理：

如果$u.\text{top}.\text{depth} < v.\text{top}.\text{depth}$，那么交换$u$和$v$，使$u$所在的树链为所处位置较深的一个。
计算$[u.\text{top}.\text{id},u.\text{id}]$的值并累加。
令$u = u.\text{top}.\text{father}$。
如果$u.\text{top} = v.\text{top}$，则转化为第一种情况。否则跳转第一步。

上面步骤的思想就是将上升期间的每一条树链的和统计出来，这样实则就是统计了这条路径上的和。
第一步的操作是为了方便后续的处理。第二步是计算这一条链上的和，包括这条链上面的一条轻边，因为在第三步中要走这条轻边到达上面一条树链。最后一步是检查是否成为了第一种情况。

下面是上面步骤的参考伪代码：

function QUERY-SUM(u, v):
    sum = 0

    // 如果不在同一条树链
    while u.top != v.top:
        if u.top.depth < v.top.depth:
            SWAP(u, v)  // 交换u和v

        sum += QUERY(u.top.id, u.id)  // 利用线段树等数据结构来求和
        u = u.top.father  // 走轻边进入上面的树链

    if u == v:  // 如果处在相同位置
        return sum

    if u.depth > v.depth:  // 使u成为深度较小的节点
        SWAP(u, v)

    return QUERY(u.next.id, v.id) + sum

如果不能理解，这里给出一个示例：
tree-splited
假设我们查询$16$到$17$：
首先会发现它们不在同一条链上，由于$16$所处的链的深度较大，为$5$，因此将$16$进行上移，上移至$14$，并统计$[13, 13]$的和。
然后$14$和$17$依然不在同一条链中，由于$14$所处的链的深度为$2$，因此将$14$上移。上移至$1$，并统计$[9, 11]$的和。
最后发现$1$和$17$已经在同一条链中了，直接统计$[1, 5]$的和即可。

修改

事实上，修改操作和查询几乎是一模一样的，只是将求和的地方变成了相应的数据结构的修改操作。这里就不再多说了。

时间复杂度

每当学习了一个新算法，我们最关切的就是它的时间复杂度了。
如果树链剖分的时间复杂度高到爆，我们写的时候估计得虚死。
但是可以证明，树链剖分后的树，从根节点到任意一个叶节点的路径只会与$O(\log n)$条树链相交。这意味着将两个节点逼近到同一条链上时，只需经过$O(\log n)$次跳转。
即基于树剖的其它操作的时间复杂度为$\Omega(\log n)$(注意是下界，具体的上界取决于操作本身的附加的复杂度)。

~~为什么会只有$O(\log n)$条呢？~~
~~我们来考虑树链剖分时最坏的情况：~~
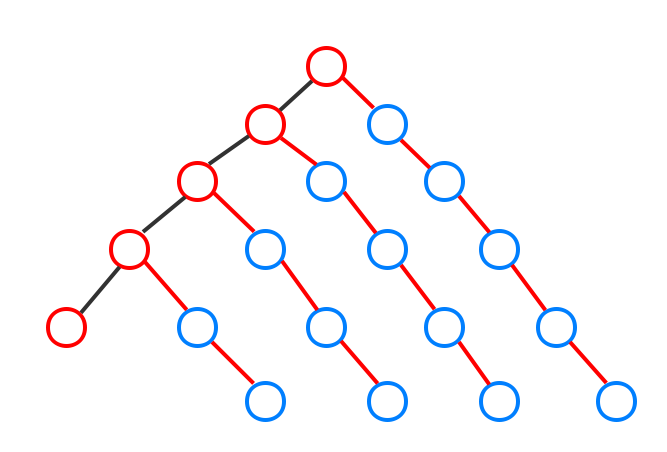
tree-worst
想象这是树剖是最坏的情况(因为实际上并不会这样)。因为树剖总是尝试将最长的剖分出来，因此树链都是向右的。如果最左链再加一个节点，树链就会向左剖分了。
~~为了达到这样的效果，这棵有根树是接近平衡的，即树高为$\Theta(\log n)$。~~
~~因此最坏的情况下，当查询最左边的节点时，只需要使用$O(\log n)$次跳转就可完成。~~

~~当然上面并不是严格的证明，只是一个形象的说明罢了。我们只需要知道树链剖分能保证很好的时间复杂度即可。~~

正确的证明思路因该是这样的：
可以考虑一棵树中轻边的数量。由于从某一个节点开始，每走一条轻边，子树的大小都会减小一倍。因此任意一条树链上只有$O(\log n)$条轻边，即意味着只有$O(\log n)$。

树链剖分计算LCA

LCA即最近公共祖先。计算LCA的算法可以说是各种各样，有暴力的爬山法，炸空间的Tarjan算法，开挂的倍增法，莫名高大上的ST跳表的搞法，还有不知所云的转成RMQ问题......在与树相关的操作中，经常需要一些求LCA的操作。其中最常用的就是倍增法，它能在$O(\log n)$的时间内求出LCA，并且其空间复杂度为$\Theta(n \log n)$。

当我们树剖后的操作需要借助到LCA时，是不是就要写个LCA的算法呢？
其实并不需要，我们可以直接利用树剖的结果来计算LCA。

然而，求LCA的过程和之前查询也是差不多的：在同一条链上的时候，深度值较小的就是LCA。如果不在同一条链上，就不断往上跳即可。这样可以在$O(\log n)$时间内求出LCA。并且仅使用了$\Theta(n)$的空间复杂度，优势十分显著。

当然，单纯拿树链剖分来求LCA也煞是浪费。既然树剖有能求LCA的能力，因此在面对需要LCA的时候就不必求助于其它的算法了。

树链剖分与DFS序

【NOI2015】软件包管理器

当我们既需要维护链上信息，又需要维护子树信息时，就有点棘手了。
维护子树信息的通常做法是DFS序。为了能够将树链剖分与DFS序结合起来，目标就是将树链剖分的编号与DFS序统一起来。
考虑到DFS序实际上不是唯一的，因此在树链剖分的过程中可以先对重儿子进行DFS，这样就可以保证一条重链上的DFS序也是递增的了。于是，我们可以继续按照DFS序维护子树的方法，同时树链剖分的信息也会被同时更新。

实际上，按照子树大小来剖分不一定能剖分出最长的树链，但这并不影响最终的操作的效率。如果要剖分出的链真正最长，应当选择秩最大的儿子作为重儿子。 ↩