[NOIP2015] 信息传递

原题题意

给你一张$ n \; (n \le 200000) $个点的有向图，请你找出其中最短的有向环，输出此环的长度。

做法

使用DFS将图遍历，找出有向环统计最小。
遍历是对节点进行标记，如果遍历中发现已经被标记的节点，则表示找到了一个环。
需要注意几点：

1. 一次DFS不一定能将整张图遍历，因此需要检查每个点，多次DFS。
2. 注意DFS的起点而导致的冲突。
   为了说明这个问题，我放一张图解释一下。
   下面是一张有向图：
   
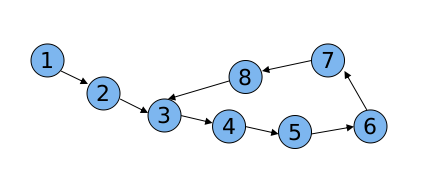
   假如我们第一次从2出发，DFS完后将2之后的点都打上了标记。
   然后从1出发继续寻找，发现2被打上了标记，会误认为是一个环，导致错误的结果。
   解决方法很简单，我们给每次DFS一个不同的编号，通常从1开始。
   我们默认如果点的标记为0表示还没有访问过。
   如果还没有访问，做的标记就是本次DFS的编号。因此，只要发现被标记的点是自己打上的，才说明发现了环。
   如果发现了别的DFS打上的标记，就不必继续搜索了。
3. 有向环的长度计算。
   这个很好办，DFS中我们维护一个$dist$数组，表示到本次搜索起点的距离。
   当发现有向环时，可以利用此数组算出来。
4. 递归优化。
   这个DFS由于不需要回溯之类的操作，并且题目中给出每个人只会将信息传给一个人，
   那么说明每个点的出度为1，因此我们可以将DFS改成递推的形式：

1
2
3
4

def dfs(s):
    while next(s) is not marked:
        # 处理s
        s = next(s)